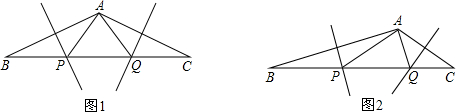如圖1，△ABC中，AB=AC，∠BAC=130°，邊AB、AC的垂直平分線交BC于點P、Q．（1）求∠PAQ的度數(shù)；（2）如圖2，△ABC中，AB＞AC，且90°＜

解：（1）∵邊AB、AC的垂直平分線交BC于點P、Q，
∴AP=BP，AQ=CQ，
∴∠BAP=∠B，∠CAQ=∠C，
∵∠BAC=130°，
∴∠B+∠C=180°-∠BAC=50°，
∴∠BAP+∠CAQ=50°，
∴∠PAQ=∠BAC-（∠BAP+∠CAQ）=130°-50°=80°；

（2）①∵邊AB、AC的垂直平分線交BC于點P、Q，
∴AP=BP，AQ=CQ，
∴∠BAP=∠B，∠CAQ=∠C，
∵∠BAC=130°，
∴∠B+∠C=180°-∠BAC=50°，
∴∠BAP+∠CAQ=50°，
∴∠PAQ=∠BAC-（∠BAP+∠CAQ）=130°-50°=80°；

∵邊AB、AC的垂直平分線交BC于點P、Q，
∴AP=BP，AQ=CQ，
∴∠BAP=∠B，∠CAQ=∠C，
∵∠BAC=α，
∴∠B+∠C=180°-∠BAC=180°-α，
∴∠BAP+∠CAQ=180°-α，
∴∠PAQ=∠BAC-（∠BAP+∠CAQ）=α-（180°-α）=2α-180°；

②當∠PAQ=90°，
即2α-180°=90°時，PA⊥AQ，
解得：α=135°，
∴當∠BAC=135°時，能使得PA⊥AQ；

③∵邊AB、AC的垂直平分線交BC于點P、Q，
∴AP=BP，AQ=CQ，
∵BC=10cm，
即BP+PQ+CQ=AP+PQ+AQ=10cm，
∴△PAQ的周長為10cm．
故